How to Implement Merge Sort in C++ with Examples

What is the merge sort? Merge sort is a comparison-based sorting algorithm that belongs to the divide and conquer category. Merge sort is used to sort an array based on the divide and conquer strategy which will be covered briefly in this post along with other concepts such as its algorithm with an example. We will also look at the time complexity of the merge sort in C++

Following pointers will be covered in this article,

• Divide and Conquer Algorithm
• Understanding the Merge sort Algorithm with an example
• Pseudocode for Merge Sort
• Program in C++ for Merge Sort
• The time complexity for Merge Sort

Moving on with this article on Merge Sort in C++

Divide and Conquer algorithm

If you are already familiar with how quicksort works you might be aware of the divide and conquer strategy. Divide and Conquer involves three major steps. For understanding these steps let’s consider an array Hello[ ] having starting index ‘a’ and ending index ‘n’ hence we can write our array in the following way Hello[a…..n ]

Divide- The prime move or the prime step of divide and conquer is to divide the given problem into sub-problems or sub-parts. The catch here is that the sub-problems should be similar to the original problem and smaller in size. In our case we will divide our array into 2 halves [a….m] [m+1…..n] m lies in the middle of a and n index

Conquer- Once we are done dividing our problem into sub-problems. We solve these subproblems recursively.

Combine- In this step, we combine all the solutions of our sub-problems in an appropriate way. In other words, we combine 2 different sorted arrays to form one sorted array. There we have our sorted array.

Moving on with this article on Merge Sort in C++

Understanding the Merge Sort Algorithm with an Example

At this point, we know what approach will be used by the merge sort. So, let’s consider an example and go through each step from Hello[ ] unsorted to a sorted array.
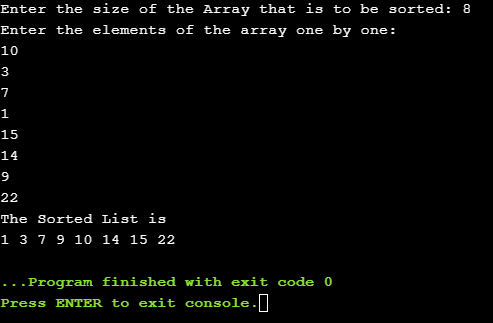
Example- Hello[10, 3, 7, 1, 15, 14, 9, 22]

In the above image, we considered an unsorted array and used merge sort to obtain a sorted array. Now, let’s look at each step and understand the whole algorithm

1. First, we considered an array Hello[10, 3, 7, 1, 15, 14, 9, 22] in this array there are total 8 elements

2. As we saw earlier merge sort uses the divide and conquer approach to sort the elements. We found m which lies in the middle of our array and divided our array from the middle where m = (a – n)/2 ‘a’ is the index of the leftmost element and n is the index of the rightmost element of our array.

3. After the first division, we have 2 parts consisting of 4 elements each. Let’s look at the first half [10, 3, 7, 1].

4. We divide [10, 3, 7, 1] in 2 parts [10, 3] and [7, 1]. After that we divide them further into [10], [3], [7], [1]. Further division is not possible as we can’t calculate m. a list containing a single element is always considered sorted.

5. How does merging take place? Let’s find out. First [10] and [3] is compared and merged in ascending order [3, 10] in the same way we get [1, 7]

6. After that, we compare [3, 10] and [1, 7]. Once compared we merge them in ascending order and We get [1, 3, 7, 10].

7. [15, 14, 9, 2] is also divided and combined in a similar way to form [9, 14, 15, 22].

8. In the last step we compare and combine [15, 14, 9, 2] [9, 14, 15, 22] to give us our sorted array i.e [1, 3, 7, 9, 10, 14, 15, 22].

Moving on with this article on Merge Sort in C++

Pseudocode for Merge Sort

Begin
   if left < right then
      m := left + (right - left) /2
      mergeSort(array, left, m)
      mergeSort (array, m+1, right)
      merge(array, left, right)
End

The function mergeSort( ) recursively calls itself to divide our array until it becomes a single element and the function merge( ) is used to merge the sorted arrays.

Moving on with this article on Merge Sort in C++

Merge sort program in C++

#include<stdlib.h> 
#include<stdio.h> 
#include<iostream>

using namespace std;

void merge(int a[], int Firstindex, int m, int Lastindex); //merges the sub-arrays which are created while division

void mergeSort(int a[], int Firstindex, int Lastindex) 
{ 
    if (Firstindex < Lastindex) 
    { 
        
        int m = Firstindex + (Lastindex - Firstindex)/2; 
  
        
        mergeSort(a, Firstindex, m); 
        mergeSort(a, m+1, Lastindex); 
  
        merge(a, Firstindex, m, Lastindex); 
    } 
}   

void merge(int a[], int Firstindex, int m, int Lastindex) 
{ 
    int x; 
    int y;
    int z;
    int sub1 = m - Firstindex + 1; 
    int sub2 =  Lastindex - m; 
  
    
    int First[sub1];  //temp array
    
    int Second[sub2]; 
  
    
    for (x = 0; x < sub1; x++) // copying data to temp arrays
        First[x] = a[Firstindex + x]; 
    for (y = 0; y < sub2; y++) 
        Second[y] = a[m + 1+ y]; 
  
    
    x = 0; 
    y = 0; 
    z = Firstindex; 
    while (x < sub1 && y < sub2) 
    { 
        if (First[x] <= Second[y]) 
        { 
            a[z] = First[x]; 
            x++; 
        } 
        else
        { 
            a[z] = Second[y]; 
            y++; 
        } 
        z++; 
    } 
    while (x < sub1) 
    { 
        a[z] = First[x]; 
        x++; 
        z++; 
    } 
    while (y < sub2) 
    { 
        a[z] = Second[y]; 
        y++; 
        z++; 
    } 
} 
int main() 
{ 
    int size;
    cout<<"Enter the size of the Array that is to be sorted: "; cin>>size;
    int Hello[size],i;
    cout<<"Enter the elements of the array one by one:n";
    for(i=0; i<size; i++) cin>>Hello[i];
    mergeSort(Hello, 0, size - 1);
    cout<<"The Sorted List isn";
    for(i=0; i<size; i++)
    {
        cout<<Hello[i]<<" ";
    }
    return 0;
}

Output-

Moving on with this article on Merge Sort in C++

Time Complexity

Time complexity is an important aspect to be considered when we talk about algorithms. Merge sort is considered to have great time complexity compared to other sorting algorithms.

Worst-case running time- O(n log n)
Best case running time- O(n log n)
Average running time- O(n log n)

With this, we come to an end of this Merge Sort in C++ article. If you wish to learn more, check out the Java Training by Edureka, a trusted online learning company. Edureka’s Java J2EE and SOA training and certification course is designed to train you for both core and advanced Java concepts along with various Java frameworks like Hibernate & Spring.

Got a question for us? Please mention it in the comments section of this blog and we will get back to you as soon as possible.