All You Need To Know About The Breadth First Search Algorithm

Graph Traversal methods have always quite fascinated me. From performing effective peer to peer communication to finding the nearest restaurants and cafes using GPS, traversal methods have a varied set of applications in the real-world scenario. In this blog on Breadth-First Search Algorithm, we will discuss the logic behind graph traversal methods and use examples to understand the working of the Breadth-First Search algorithm.

To get in-depth knowledge of Artificial Intelligence and Machine Learning, you can enroll for live Machine Learning Engineer Master Program by Edureka with 24/7 support and lifetime access.

Here’s a list of topics that will be covered in this blog:

1. Introduction To Graph Traversal
2. What is the Breadth-First Search?
3. Understanding the Breadth-First Search algorithm with an example
4. Breadth-First Search Algorithm Pseudocode
5. Applications Of Breadth-First Search

Introduction To Graph Traversal 

The process of visiting and exploring a graph for processing is called graph traversal. To be more specific it is all about visiting and exploring each vertex and edge in a graph such that all the vertices are explored exactly once.

That sounds simple! But there’s a catch.

There are several graph traversal techniques such as Breadth-First Search, Depth First Search and so on. The challenge is to use a graph traversal technique that is most suitable for solving a particular problem. This brings us to the Breadth-First Search technique.

Top 10 Trending Technologies to Learn in 2025 | Edureka

 

This video talks about the Top 10 Trending Technologies in 2025 that you must learn.

What is the Breadth-First Search Algorithm?

Breadth-First Search algorithm is a graph traversing technique, where you select a random initial node (source or root node) and start traversing the graph layer-wise in such a way that all the nodes and their respective children nodes are visited and explored.

Before we move further and understand Breadth-First Search with an example, let’s get familiar with two important terms related to graph traversal:

1. Visiting a node: Just like the name suggests, visiting a node means to visit or select a node.
2. Exploring a node: Exploring the adjacent nodes (child nodes) of a selected node.

Refer the above figure to better understand this.

Check out this Artificial Intelligence Course by Edureka to upgrade your AI skills to the next level.

Understanding the Breadth-First Search Algorithm with an example

Breadth-First Search algorithm follows a simple, level-based approach to solve a problem. Consider the below binary tree (which is a graph). Our aim is to traverse the graph by using the Breadth-First Search Algorithm.

Before we get started, you must be familiar with the main data structure involved in the Breadth-First Search algorithm.

A queue is an abstract data structure that follows the First-In-First-Out methodology (data inserted first will be accessed first). It is open on both ends, where one end is always used to insert data (enqueue) and the other is used to remove data (dequeue). 

Now let’s take a look at the steps involved in traversing a graph by using Breadth-First Search:

Step 1: Take an Empty Queue.

Step 2: Select a starting node (visiting a node) and insert it into the Queue.

Step 3: Provided that the Queue is not empty, extract the node from the Queue and insert its child nodes (exploring a node) into the Queue.

Step 4: Print the extracted node.

Don’t worry if you’re confused, we shall understand this with an example.

Take a look at the below graph, we will use the Breadth-First Search algorithm to traverse through the graph.

In our case, we’ll assign node ‘a’ as the root node and start traversing downward and follow the steps mentioned above.

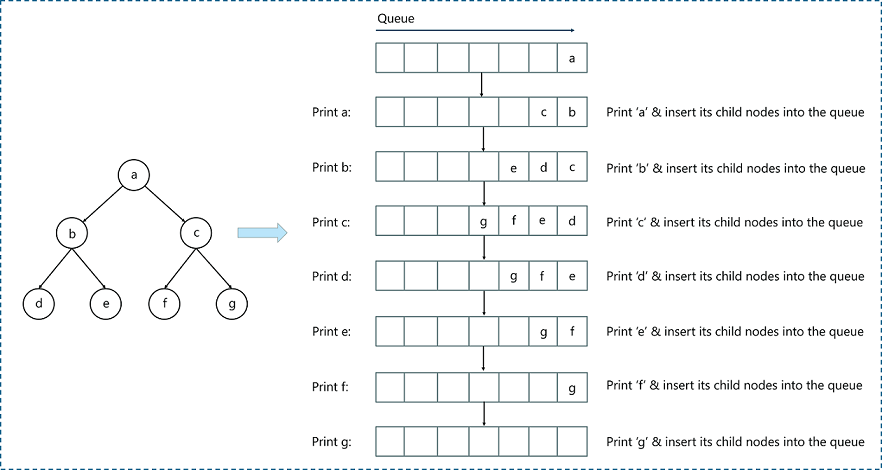
The above image depicts the end-to-end process of Breadth-First Search Algorithm. Let me explain this in more depth.

1. Assign ‘a’ as the root node and insert it into the Queue.
2. Extract node ‘a’ from the queue and insert the child nodes of ‘a’, i.e., ‘b’ and ‘c’.
3. Print node ‘a’.
4. The queue is not empty and has node ‘b’ and ‘c’. Since ‘b’ is the first node in the queue, let’s extract it and insert the child nodes of ‘b’, i.e., node ‘d’ and ‘e’.
5. Repeat these steps until the queue gets empty. Note that the nodes that are already visited should not be added to the queue again.

Now let’s look at the pseudocode of Breadth-First Search algorithm.

Breadth-First Search Algorithm Pseudocode

Here’s the pseudocode to implement the Breadth-First Search Algorithm:

In the above code, the following steps are executed:

1. (G, s) is input, here G is the graph and s is the root node
2. A queue ‘Q’ is created and initialized with the source node ‘s’
3. All child nodes of ‘s’ are marked
4. Extract ‘s’ from queue and visit the child nodes
5. Process all the child nodes of v
6. Stores w (child nodes) in Q to further visit its child nodes
7. Continue till ‘Q’ is empty

Before we wrap up the blog, let’s look at some applications of Breadth-First Search algorithm.

Applications Of Breadth-First Search Algorithm

Breadth-first Search is a simple graph traversal method that has a surprising range of applications. Here are a few interesting ways in which Bread-First Search is being used:

Crawlers in Search Engines: Breadth-First Search is one of the main algorithms used for indexing web pages. The algorithm starts traversing from the source page and follows all the links associated with the page. Here each web page will be considered as a node in a graph.

GPS Navigation systems: Breadth-First Search is one of the best algorithms used to find neighboring locations by using the GPS system.

Find the Shortest Path & Minimum Spanning Tree for an unweighted graph: When it comes to an unweighted graph, calculating the shortest path is quite simple since the idea behind shortest path is to choose a path with the least number of edges. Breadth-First Search can allow this by traversing a minimum number of nodes starting from the source node. Similarly, for a spanning tree, we can use either of the two, Breadth-First Search or Depth-first traversal methods to find a spanning tree.

Broadcasting: Networking makes use of what we call as packets for communication. These packets follow a traversal method to reach various networking nodes. One of the most commonly used traversal methods is Breadth-First Search. It is being used as an algorithm that is used to communicate broadcasted packets across all the nodes in a network.

Peer to Peer Networking: Breadth-First Search can be used as a traversal method to find all the neighboring nodes in a Peer to Peer Network. For example, BitTorrent uses Breadth-First Search for peer to peer communication.

So that was all about the working of the Breadth-First Search algorithm. Now that you know how to traverse graphs, I’m sure you’re curious to learn more. Here are a few relevant blogs to keep you interested:

1. A Complete Guide To Maths And Statistics For Data Science
2. All You Need To Know About Statistics And Probability
3. Introduction To Markov Chains With Examples – Markov Chains With Python
4. How To Implement Bayesian Networks In Python? – Bayesian Networks Explained With Examples

With this, we come to the end of this blog. If you have any queries regarding this topic, please leave a comment below and we’ll get back to you.