How To Implement Merge Sort in C?

Merge Sort is one of the best examples of Divide & Conquer algorithm. This article will help you understand Merge Sort In C in depth. Following pointers will be covered in this article,

• Merge Sort Algorithm
• Example
• Merge Sort Function in C
• Merge Function in C
• Merge Sort C Program
• Merge Sort Function in C
• Functions to Print Elements of Array
• Main Method

So let us begin

Before we discuss about Merge sort algorithm, let us understand Divide & Conquer technique. In Divide & Conquer algorithm design paradigm, we divide the problems in sub-problems recursively then solve the sub-problems, & at last combine the solutions to find the final result.
One thing to keep in mind while dividing the problems into sub-problems is that, the structure of sub-problems should not change as of the original problem.
Divide & Conquer algorithm has 3 steps:
1. Divide: Breaking the problem into subproblems
2. Conquer: Recursively solving the subproblems
3. Combine: Combining the solutions to get the final result

In Merge sort, we divide the array recursively in two halves, until each sub-array contains a single element, and then we merge the sub-array in a way that it results into a sorted array. merge() function merges two sorted sub-arrays into one, wherein it assumes that array[l .. n] and arr[n+1 .. r] are sorted.

Merge sort is one of the efficient & fastest sorting algorithms with the following time complexity:

Worst Case Time Complexity: O(n*log n)
Best Case Time Complexity: O(n*log n)
Average Time Complexity: O(n*log n)

Moving on with this article on Merge Sort in C

Merge Sort Algorithm

MergeSort(arr[], l, r), where l is the index of the first element & r is the index of the last element.
If r > l
1. Find the middle index of the array to divide it in two halves:
m = (l+r)/2
2. Call MergeSort for first half:
mergeSort(array, l, m)
3. Call mergeSort for second half:
mergeSort(array, m+1, r)
4. Recursively, merge the two halves in a sorted manner, so that only one sorted array is left:
merge(array, l, m, r)

Moving on with this article

Example:

1. Divide the unsorted array recursively until 1 element in each sub-array remains.

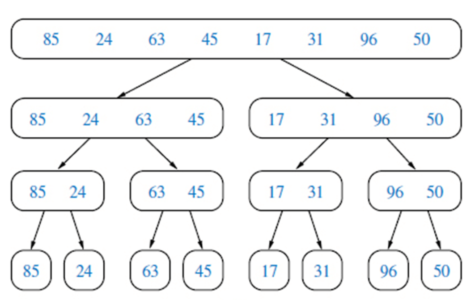
2. Recursively, merge sub-arrays to produce sorted sub-arrays until all the sub-array merges and only one array remains.

To sort an array using Merge sort, following is the process
We take two variables p & r where p stores the staring index & stores the last index of the array
Next, we find the mid of the array to break it in two halves. Formula yo do so is (p+r)/2 and mark the middle element as m.
Next step is to break the given array into two subarrays from the middle element, i.e. from index p to m & m+1 to r.
We continue to break the subarrays until we reach to a level where each sub array contains 1 element.
Next we merge the sub-array recursively in a sorted order, so that we finally get a sorted array.

Moving on with this article on Merge Sort in C

Merge Sort Function in C

void mergeSort(int arr[], int l, int r)
{
if (l < r)
{
// Finding mid element
int m = l+(r-l)/2;
// Recursively sorting both the halves
mergeSort(arr, l, m);
mergeSort(arr, m+1, r);

// Merge the array
merge(arr, l, m, r);
}
}

Moving on with this article

Merge Function in C

void merge(int arr[], int l, int m, int r)
{
int i, j, k;
int n1 = m - l + 1;
int n2 = r - m;
// Create temp arrays
int L[n1], R[n2];
// Copy data to temp array
for (i = 0; i < n1; i++)
L[i] = arr[l + i];
for (j = 0; j < n2; j++)
R[j] = arr[m + 1+ j];
// Merge the temp arrays
i = 0;
j = 0;
k = l;
while (i < n1 && j < n2)
{
if (L[i] <= R[j])
{
arr[k] = L[i];
i++;
}
else
{
arr[k] = R[j];
j++;
}
k++;
}
// Copy the remaining elements of L[]
while (i < n1)
{
arr[k] = L[i];
i++;
k++;
}
// Copy the remaining elements of R[]
while (j < n2)
{
arr[k] = R[j];
j++;
k++;
}
}

Moving on with this article on Merge Sort in C

Merge Sort C Program

#include<stdlib.h>
#include<stdio.h>
// Merge Function
void merge(int arr[], int l, int m, int r)
{
int i, j, k;
int n1 = m - l + 1;
int n2 = r - m;
int L[n1], R[n2];
for (i = 0; i < n1; i++)
L[i] = arr[l + i];
for (j = 0; j < n2; j++)
R[j] = arr[m + 1+ j];
i = 0;
j = 0;
k = l;
while (i < n1 && j < n2)
{
if (L[i] <= R[j])
{
arr[k] = L[i];
i++;
}
else
{
arr[k] = R[j];
j++;
}
k++;
}
while (i < n1)
{
arr[k] = L[i];
i++;
k++;
}
while (j < n2)
{
arr[k] = R[j];
j++;
k++;
}
}

Moving on with this article

// Merge Sort Function in C

void mergeSort(int arr[], int l, int r)
{
if (l < r)
{
int m = l+(r-l)/2;
mergeSort(arr, l, m);
mergeSort(arr, m+1, r);
merge(arr, l, m, r);
}
}

Moving on with this article on Merge Sort in C

// Functions to Print Elements of Array

void printArray(int A[], int size)
{
int i;
for (i=0; i < size; i++)
printf("%d ", A[i]);
printf("n");
}

Moving on with this article on Merge Sort in C

// Main Method

int main()
{
int arr[] = {85, 24, 63, 45, 17, 31, 96, 50};
int arr_size = sizeof(arr)/sizeof(arr[0]);
printf("Given array is n");
printArray(arr, arr_size);
mergeSort(arr, 0, arr_size - 1);
printf("nSorted array is n");
printArray(arr, arr_size);
return 0;
}

Output:

Now after executing the above C program you would have understood how Merge Sort works & how to implement it in C. I hope this blog is informative and added value to you.

With this we come to the end of this blog on ‘Merge Sort In C’. I hope you found this informative and helpful, stay tuned for more tutorials on similar topics.

You may also checkout our training program to get in-depth knowledge on jQuery along with its various applications, you can enroll here for live online training with 24/7 support and lifetime access.Implement the above code with different strings and modifications. Now, we have a good understanding of all key concepts related to the pointer.

Got a question for us? Mention them in the comments section of  this blog and we will get back to you.