Binary Search In C: Everything You Need To Know Binary Search

Searching Algorithms are very important as they help search data in patterns which is otherwise very difficult. In this article we will take take a look at Binary Search in C with practical implementation. Following Pointers will be covered in this article:

• Binary Search In C
• Example 1
• Example 2

Let us get started with article on Binary Search in C,

Binary Search In C

A Binary Search is a sorting algorithm, that is used to search an element in a sorted array. A binary search technique works only on a sorted array, so an array must be sorted to apply binary search on the array. It is a searching technique that is better then the liner search technique as the number of iterations decreases in the binary search.

The logic behind the binary search is that there is a key. This key holds the value to be searched. The highest and the lowest value are added and divided by 2. Highest and lowest and the first and last element in the array. The mid value is then compared with the key. If mid is equal to the key, then we get the output directly. Else if the key is greater then mid then the mid+1 becomes the lowest value and the process is repeated on the shortened array. Else if the key value is less then mid, mid-1 becomes the highest value and the process is repeated on the shortened array. If it is not found anywhere, an error message is displayed.

Let us move further with this Binary Search In C article and see an example,

Example 1

Let’s look at the code:

#include <stdio.h>
int main()
{
int i, low, high, mid, n, key, array[100];
printf("Enter number of elementsn");
scanf("%d",&n);
printf("Enter %d integersn", n);
for(i = 0; i < n; i++)
scanf("%d",&array[i]);
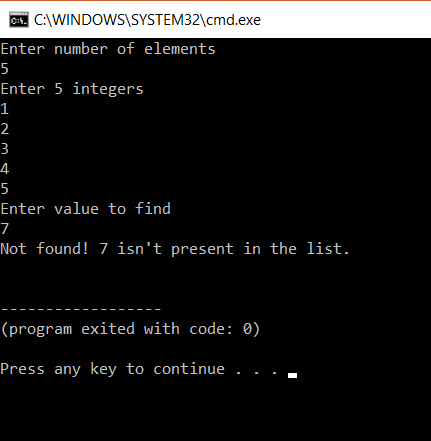
printf("Enter value to findn");
scanf("%d", &key);
low = 0;
high = n - 1;
mid = (low+high)/2;
while (low <= high) {
if(array[mid] < key)
low = mid + 1;
else if (array[mid] == key) {
printf("%d found at location %d.n", key, mid+1);
break;
}
else
high = mid - 1;
mid = (low + high)/2;
}
if(low > high)
printf("Not found! %d isn't present in the list.n", key);
return 0;
}

Output:

If the key is present:

If Key is not present:

In the program above, We declare i, low, high, mid, n, key, array[100].

• i is used for iteration through the array.
• low is used to hold the first array index.
• high is used to hold the last array index.
• mid holds the middle value calculated by adding high and low and dividing it by 2.
• n is the number of elements in the array.
• key is the element to search.
• array is the array element of size 100.

We first, take in the number of elements the user array needs and store it in n. Next, we take the elements from the user. A for loop is used for this process. Then, we take the number to be searched from the array and store it in the key.

Next, we assign 0 to the low variable which is the first index of an array and n-1 to the high element, which is the last element in the array. We then calculate the mid value.    mid = (low+high)/2 to get the middle index of the array.

There is a while loop which checks if low is less then high to make sure that the array still has elements in it. If low is greater then, high then the array is empty. Inside the while loop, we check whether the element at the mid is less than the key value(array[mid] < key).  If yes, then we assign low the value of mid +1 because the key value is greater then mid and is more towards the higher side. If this is false, then we check if mid is equal to key. If yes, we print and break out of the loop. If these conditions don’t match then we assign high the value of mid-1, which means that the key is smaller than mid.

The last part checks if low is greater then high, which means there are no more elements left in the array.

Remember, this algorithm won’t work if the array is not sorted.

Let us move to the final bit of this Binary Search In C article

Example 2

Binary Search Using Recursive Function:

Code:

#include <stdio.h>
int binaryScr(int a[], int low, int high, int m)
{
if (high >= low) {
int mid = low + (high - low) / 2;
if (a[mid] == m)
return mid;
if(a[mid] > m)
return binaryScr(a, low, mid - 1, m);
return binaryScr(a, mid + 1, high, m);
}
return -1;
}
int main(void)
{
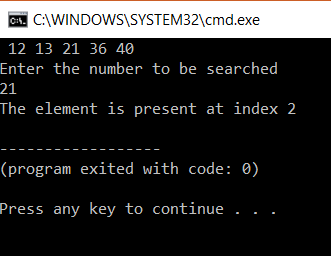
int a[] = { 12, 13, 21, 36, 40 };
int i,m;
for(i=0;i<5;i++)
{
printf(" %d",a[i]);
}
printf(" n");
int n = sizeof(a) / sizeof(a[0]);
printf("Enter the number to be searchedn");
scanf("%d", &m);
int result = binaryScr(a, 0, n - 1, m);
(result == -1) ? printf("The element is not present in array")
printf("The element is present at index %d",
result);
return 0;
}

OUTPUT:

In the above program, we use a function BinaryScr to search the element in the array. The function is recursively called to search the element.

We accept the input from the user and store it in m. We have declared and initialized the array. We send the array, the lower index, higher index and the number to be searched to the BinaryScr function and assign it to result. In the function, it performs binary search recursively. If not found, then it returns -1. In the main function, the ternary operator is used. If result=-1 then not found else found is displayed.

With this we come to the end of this blog on ‘Binary Search In C’. I hope you found this informative and helpful, stay tuned for more tutorials on similar topics.You may also checkout our training program to get in-depth knowledge on jQuery along with its various applications, you can enroll here for live online training with 24/7 support and lifetime access.

Got a question for us? Mention them in the comments section of  this blog and we will get back to you.